In my first post about Unity surface shaders, I’ll explain the basics of lighting and vector math.

What is a shader?

A shader is a small program that tells you what color any given point on the surface of an object will appear on screen.

It’s mostly about angles and distances. The color will probably vary based on the angle of the surface relative to the light, and frequently the angle of the surface relative to the camera and the distance of the point from the camera.

So let’s start with some simple lighting.

Reflections

When light hits a surface, different things happen to it based on the nature of the surface being hit.

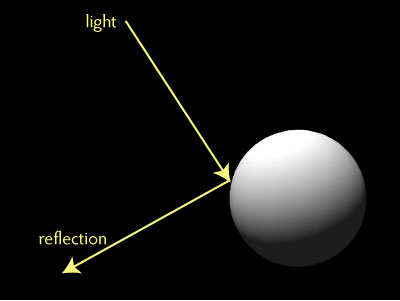
When light hits a mirror, it reflects in a very predictable way; every incoming ray of light bounces off of the mirror, like a rubber bouncy ball hitting a smooth surface.

For other surfaces, the light can — and will — go off in pretty much any direction. It’s kind of like bouncing that ball off of a rocky surface: it’s going to be harder to predict where the ball will go.

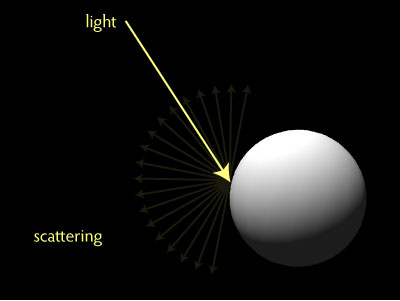
You can think of the light as bouncing off the surface in all directions simultaneously. This is called scattering.

For our first shader, we’ll make a scattery sort of surface — because writing that will be simpler than a shiny surface. Since the light is being reflected in all directions, it doesn’t matter where the viewer is.

Diffuse Reflectons

To write this shader, we just care about three things:

• The albedo of the surface. Albedo is the color a surface is, regardless of what color or intensity light is shining on it.
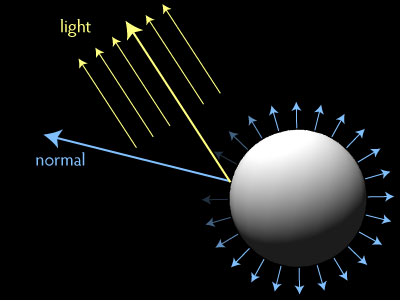
• The normal of the surface. You can think of a normal as an arrow pointing straight out of a surface, telling you the orientation of the surface.
• The direction to the light source we’re interested in.

The way this lighting model works is, if the normal is pointing in the same direction as the arrow going to the light, the surface will appear bright; if the normal and the arrow to the light are perpendicular or pointing in opposite directions, the surface will be dark.

But how do we measure how similar two directions are? That’s where vector math comes in.

Vectors!

A vector represents a direction, and it can have a magnitude — a length — associated with it.

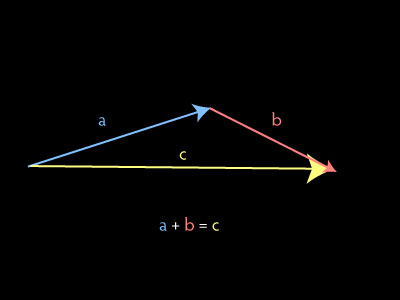
Like numbers, vectors can be added together.

Note that vectors don’t represent a line going from somewhere to somewhere — vectors are just about directions. Where you started from is irrelevant.

For everything — absolutely everything — we’re going to do with vectors, we don’t care about the magnitude. Or, rather, we want to work with unit vectors: vectors with a magnitude of 1.

So back to that similarity problem: what makes one vector more or less similar to another? We can say ‘if they’re pointing close to the same direction, they’re similar’, but how do we define that precisely?

For this, we need a dot product. A dot product is an operation you can do on two vectors, the way you can add numbers or multiply numbers.

But unlike addition, dot products have no clear analog to numbers. And the dot product of two vectors is not another vector — it’s a number.

Mathematically speaking, the dot product of two vectors is equal to the product of the lengths of the vectors, multiplied by the cosine of the angle between them.

For unit vectors, then, the dot product is just the cosine of the angle between the vectors. So for identical vectors,  with an angle of 0, the cosine is 1, and for vectors at a 90 degree angle to each other the cosine is 0. This is the relationship we’re looking for.

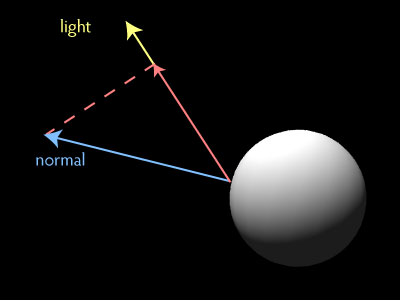
To express this in more visual terms you can think of it as ‘dropping’ one vector onto another.

So here we’ve got normal and light direction vectors.  The dashed line goes through the endpoint of the normal vector and is perpendicular to the light vector. At the point where the dashed line and light vector meet, I’m making a new vector. It’s sort of a projection of the normal onto the light vector.

The length of this vector is the amount of light we see on our surface.

So there are some basic lighting concepts. In my next post. I’ll show you how to translate these concepts into a real shader.